Rotation01: Euler Angles and Rotation Matrix
In the field of robot localization, we typically use rotation and translation to represent the robot’s pose (position and orientation), which is basic knowledge. If this part is not thoroughly understood, even when using libraries, not understanding the transformation relationships between coordinate systems can significantly reduce work efficiency. Translation (position) is represented using a three-dimensional coordinate in the Cartesian coordinate system, which may be basic knowledge at the middle school level or even lower. Therefore, what really needs to be supplemented is the expression of rotation (orientation) in three-dimensional space.
At the beginner stage, many introductory tutorials, such as “视觉SLAM十四讲“, have already explained things clearly, covering topics like rotation matrices, quaternions, axis-angle representation, euler angles, and the nightmarish Lie algebra, as well as the derivations of their conversion relationships. However, in my work of localization and mapping, I found that the transformation relationships between these various representations can mostly be solved by simply calling functions from the Eigen or tf libraries.
What comes up most frequently in projects is actually the problem of gimbal lock with Euler angles, because using Euler angles to understand rotations is really intuitive for humans. You could explain it to someone on a construction site, and they’d understand what you mean. The most important thing to be cautious about is relative poses in different coordinate systems, because it’s really easy to get confused. What we need to deeply learn and consolidate are the mathematical concepts related to manifolds, groups, and Lie algebra, because I believe we won’t be satisfied with just being a ‘cute library user’ (even if I am one, I’m still proud of it:cry).”
Although it’s very basic, it’s truly the foundation of the structure. So let’s go through it once more and make this note.
Begin from Euler Angles
Unlike the order in ‘The Fourteen Lectures,’ here we start with Euler angles because they are indeed the most intuitive way to represent rotations. Euler angles represent rotations around the three coordinate axes (ZYX) by the following angles: Yaw , Pitch, and Roll. However, it is important to note that the order of the axes must be fixed, because each rotation happens relative to the axis after the previous rotation. As shown in the figure below, the example here demonstrates the ZYX order.
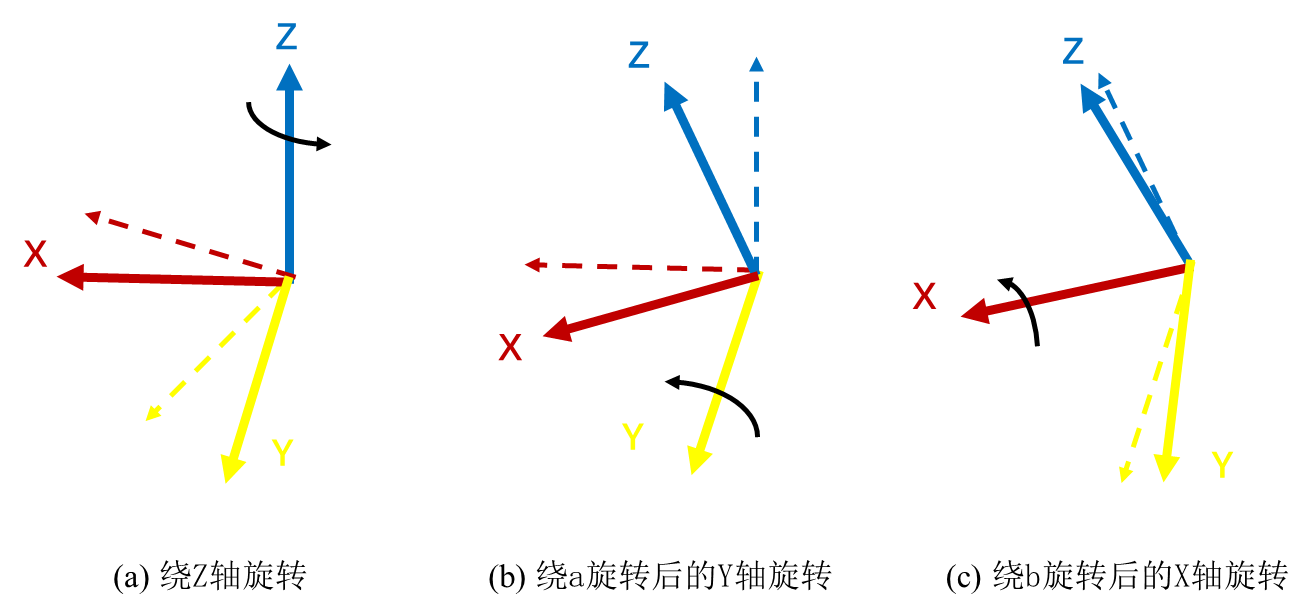
Gimbal Lock
When we mention Euler angles, the first thing that comes to mind is the Gimbal Lock problem. Maybe it’s because I have poor spatial awareness, so I couldn’t figure out the problem just by rotating a model for a while. I watched some videos and even though they had high view counts, they didn’t seem to explain it very clearly. It wasn’t until I saw a demonstration of a gimbal setup that I truly understood the process. Also, I found a highly upvoted comment by ‘yyhhhyeah’ on this Bilibili video, which helped clarify things for me. I’ve included the quote here:
“说了一大堆,其实就是在说一件事:欧拉角描述相对于初始状态的变换,只和最终状态有关,与过程无关。 ”
“所谓的万向死锁,这个名字很具有误导性,听起来像是欧拉角这种描述方式存在巨大缺陷一样。其本质就是:物体角度状态与欧拉角坐标并非一一对应关系。某些位置状态并不唯一确定一组欧拉角坐标”
Why can’t it be just rotating around two axes?
We know that in three-dimensional space, rotation has three degrees of freedom, so at least three parameters are needed to describe a rotation. This is an undeniable fact. My confusion doesn’t actually lie in this point, but rather in the limitations of my spatial imagination.
‘For a plane coordinate system, it’s clear that rotating around one axis can represent all rotation states. One full rotation around an axis just traces a circle; so, when this idea is extended to three-dimensional space, it seems that using a sphere can represent all possible orientations. Later, I realized that actually, rotating around two axes can also cover the entire sphere.’
At that point, my mind got stuck in the conflict between theory and intuition. Although I knew this wasn’t entirely correct, I kept wondering if it was possible to express all orientations by rotating around two axes.
Looking back, this was actually a very simple mistake. Even now, I don’t understand why I turned the problem into a model of a spherical shell. The solution is very straightforward: aside from the axis that points to the sphere, we still have two other axes left, and once the object is oriented toward the sphere, how do we handle its rolling? Once that issue was solved, I finally understood.
From Euler Angles to Rotation Matrix
When writing parameter configuration files, I prefer to have the program read Euler angles because they are intuitive and allow me to easily understand the extrinsic parameters between different sensors. After the code file imports these parameters, I convert them into the Eigenrotation matrix format for further processing. Now, let’s derive the formula from Euler angles to the rotation matrix in a simple way. To save effort, let’s start with two dimensions. Assume we have a point $P(x,y)$ that is transformed from a vehicle coordinate system $O$ to another world coordinate system $W$:$\varphi$ is the angle of rotation from $W$ to $O$,$r$ is the distance from the point to the origin, and $\theta$ is the angle between the point and the $X$-axis of the vehicle coordinate system $O$.
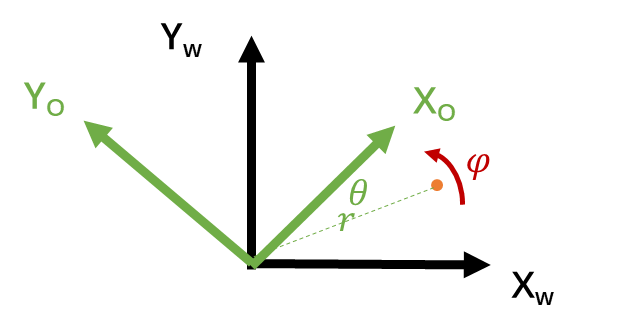
then,
\[x_w = x_o\cos(\varphi) - y_o\sin(\varphi) \\ y_w = x_o\sin(\varphi) + y_o\cos(\varphi) \tag {2}\]so,
\[\begin{bmatrix} x_w \\ y_w \\ \end{bmatrix} = \begin{bmatrix} \cos(\varphi) & -\sin(\varphi) \\ \sin(\varphi) & \cos(\varphi) \\ \end{bmatrix} \begin{bmatrix} x_o \\ y_o \\ \end{bmatrix}\tag{3}\]The term in the middle is the rotation matrix $R_{wo}$,which represents the rotation relationship from the vehicle coordinate system $O$ to the world coordinate system $W$, By combining this rotation matrix $R_{wo}$ with the translation vector $t_{wo}$, we can describe the pose of the vehicle coordinate system $O$ relative to the world coordinate system.
Expanding to the three-dimensional case, based on the definition of Euler angles we mentioned earlier:
- Rotation angle $\alpha$ around the $Z$-axis (Yaw), corresponding to the rotation matrix:
- Rotation angle $\beta$ around the $Y$-axis (Pitch), corresponding to the rotation matrix:
- Rotation angle $\gamma$ around the $X$-axis (roll), corresponding to the rotation matrix:
By using the closure property of matrix multiplication and performing successive multiplication, we can obtain the rotation matrix from the Euler angles:
\[R = R_z(\alpha) \cdot R_y(\beta) \cdot R_x(\gamma) \tag{7}\]“视觉SLAM十四讲”’ derive the rotation matrix and its properties step by step starting from the orthonormal basis in linear algebra. The process will not be repeated here. What we need to remember about the rotation matrix is its orthogonality($R^TR=I$)and that its determinant is 1. These properties can be verified in equations$(4)(5)(6)(7)$. Why are these properties important? It’s because they are closely related to the concept of groups discussed later.
However, using the two methods we discussed above to represent rotations seems to be already quite perfect. Euler angles help us intuitively visualize rotation, and rotation matrices provide a multiplication-closed representation of rotation and the associated mathematical computation rules. So what is the significance of other methods? The answer is that rotation matrices, which do not satisfy closure under addition, cannot meet the differentiation requirements. The essence of the SLAM problem is feature matching and state estimation. If you’re familiar with the least squares process, you’ll realize that if we can’t differentiate, how can we complete state estimation?
Therefore, knowledge of quaternions and groups is extremely important, and we will revisit this topic in detail later.