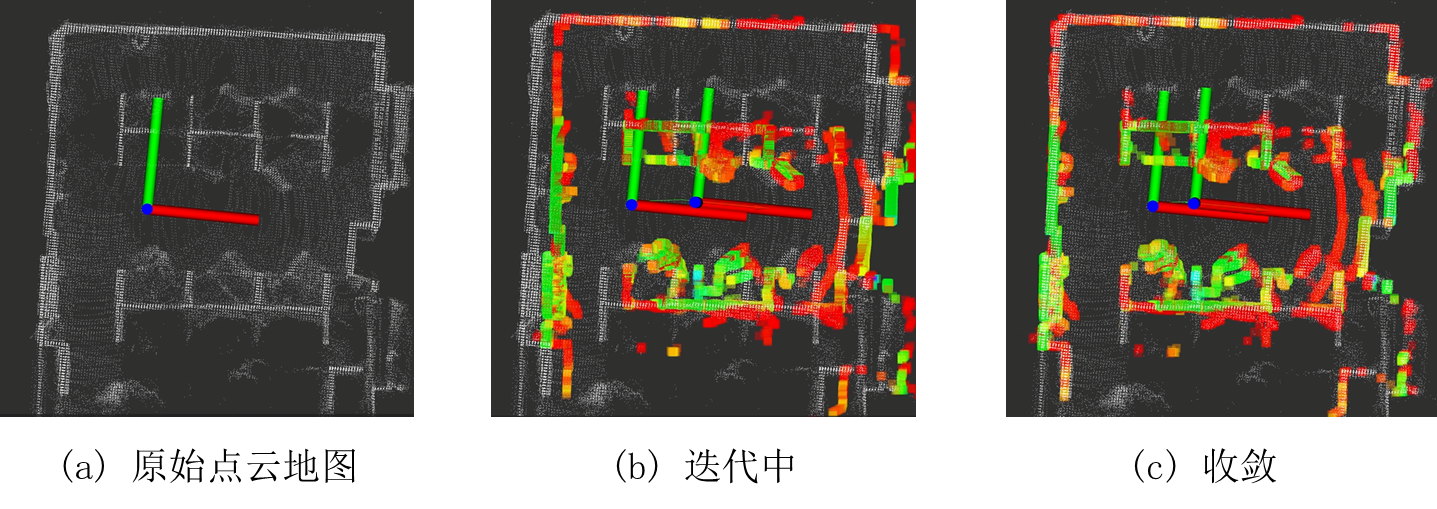
Taylor expansion of a Multi-dimensional function
The Taylor expansion of a function expands a nonlinear function at a certain point to obtain a polynomial that can approximate the original function well near that point. Taylor expansion is very useful in numerically solving nonlinear equations.
Taylor expansion of a one-dimensional function
\[f(x_{k+1})=f(x_k + \Delta x)=f(x_k) + \frac{f'(x_k)}{1!}\Delta x + \frac{f^{2}(x_k)}{2!}\Delta x^2 + o(n) \tag 1\]Amazing formula~
Taylor expansion of a two-dimensional function
\[f(x_{k+1},y_{k+1})=f(x_k + \Delta x,y_k + \Delta y) \\ =f(x_{k},y_{k})\\ + \frac{f'_{x}(x_{k},y_{k})}{1!}\Delta x+ \frac{f'_{y}(x_{k},y_{k})}{1!}\Delta y \\ + \frac{f^2_{xx}(x_{k},y_{k})}{2!}(\Delta x)^2 + \frac{f^2_{yy}(x_{k},y_{k})}{2!}(\Delta y)^2+ \frac{f_{xy}^{2}(x_{k},y_{k})}{2!}\Delta x\Delta y + \frac{f_{yx}^{2}(x_{k},y_{k})}{2!}\Delta x\Delta y \\ + o(n) \tag 2\]Writing the first three terms in matrix form, we have:
\[f(x_k + \Delta x,y_k + \Delta y) =f(x_{k},y_{k}) + \begin{bmatrix}f'_{x}(x_{k},y_{k}) \\ f'_{y}(x_{k},y_{k}) \end{bmatrix}^T\begin{bmatrix}\Delta x \\ \Delta y \end{bmatrix} +\begin{bmatrix}\Delta x \\ \Delta y \end{bmatrix}^T\begin{bmatrix}f^{(2)}_{xx}(x_{k},y_{k}) & f^{(2)}_{xy}(x_{k},y_{k}) \\ f^{(2)}_{yx}(x_{k},y_{k}) & f^{(2)}_{yy}(x_{k},y_{k}) \end{bmatrix}^T \begin{bmatrix}\Delta x \\ \Delta y \end{bmatrix} \tag 3\]Taylor expansion of a Multi-dimensional function
\[f(X)=f(X + \Delta X) \\ =f(X)+ \sum_{i = 1}^{n}\frac{f'_{x^i}(X)}{1!}\Delta x^i + \sum_{i,j=0}^n\frac{f_{x^ix^j}^{2}(X)}{2!}\Delta x^i \Delta x^j + o(n) \tag 4\]As what we have done, the first three terms
\[f(X + \Delta x) =f(X) + \begin{bmatrix}f'_{x^1}(X) \\ f'_{x^2}(X) \\ \vdots \\ f'_{x^n}(X) \end{bmatrix}^T \Delta X +\Delta X^T\begin{bmatrix}f^{(2)}_{x^1x^1}(X) & \cdots &f^{(2)}_{x^1x^n}(X) \\ \vdots & \ddots & \vdots\\ f^{(2)}_{x^nx^1}(X) &\cdots & f^{(2)}_{x^nx^n}(X) \end{bmatrix}^T \Delta X \tag 5\]finish~