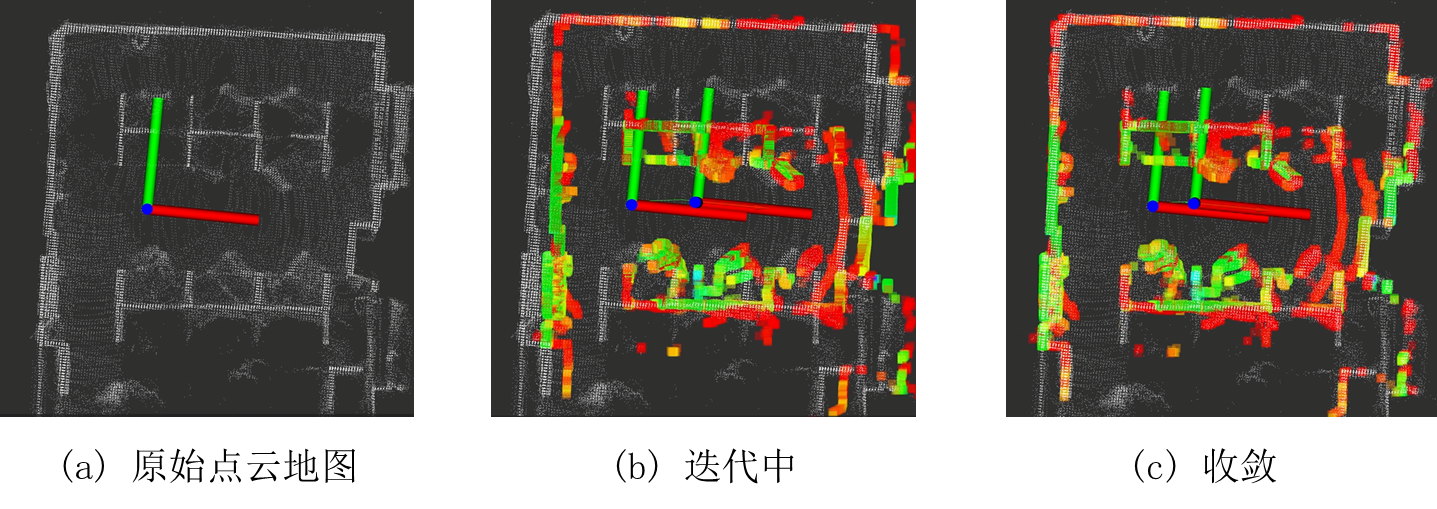
Unconstrained Optimization: Gauss-Newton Method
The role of unconstrained optimization in robotics is unquestionable. This blog simply records the derivation of the Gauss-Newton method in unconstrained nonlinear optimization methods.
Begin from the least squares
\[min \ F(x) = \frac{1}{2}||f(x)||_2^2 \tag{1}\]Perform Taylor expansion on $f(x)$:
\[f(x_0 + \Delta x) = f(x_0) + J(x_0) \Delta x + \Delta x^T\frac{H(x_0)}{2}\Delta x + o(n) \tag 2\]Here we consider $f$ to be the mapping of the $m$-dimensional vector $x_0$ to the $m$-dimensional error term, $\Delta x$ is the change, $J(x_0)$ is the Jacobian matrix, and $H(x_0)$ is the Hessian matrix.
Keep only first-order terms:
\[min \ F(x) =\frac{1}{2}[f(x_0) + J(x_0) \Delta x]^T[f(x_0) + J(x_0) \Delta x] \\ =\frac{1}{2}[||f(x_0)||_2^2 + 2\Delta x^T J(x_0)^T f(x_0) + \Delta x^T J(x_0)^T J(x_0) \Delta x] \tag 3\]Obviously, if you want to get the minimum value, you need to find the partial derivative of $\Delta x$:
\[\frac{\partial F(x)}{\partial \Delta x} = J(x_0)^T f(x_0) + J(x_0)^T J(x_0) \Delta x = 0 \tag 4\]so,
\[\Delta x = -[J(x_0)^T J(x_0)]^{-1}J(x_0)^T f(x_0) \tag{5}\]Introducing the Information Matrix
In the actual modeling process, the inverse of the covariance is derived as the information matrix, which is used as the weight to characterize the size of each item:
\[min \ F(x) = \frac{1}{2}f(x)^T \Sigma^{-1} f(x) \tag{6}\]Same as before,
\[min \ F(x) =\frac{1}{2}[f(x_0) + J(x_0) \Delta x]^T \Sigma^{-1} [f(x_0) + J(x_0) \Delta x] \\ =\frac{1}{2}[f(x_0)^T \Sigma^{-1} f(x_0) + 2\Delta x^T J(x_0)^T \Sigma^{-1} f(x_0) + \Delta x^T J(x_0)^T \Sigma^{-1}J(x_0) \Delta x] \tag 7\] \[\frac{\partial F(x)}{\partial \Delta x} = J(x_0)^T \Sigma^{-1} f(x_0) + J(x_0)^T \Sigma^{-1} J(x_0) \Delta x = 0 \tag 8\] \[\Delta x = -[J(x_0)^T \Sigma^{-1} J(x_0)]^{-1}J(x_0)^T \Sigma^{-1} f(x_0) \tag{9}\]Batch Least Squares
When there are multiple error terms:
\[min \ F(x) =\sum_i \frac{1}{2}f_i(x)^T \Sigma_i^{-1} f_i(x) \tag{10}\]Same as before,
\[min \ F(x) =\sum_i\frac{1}{2}[f_i(x_0) + J_i(x_0) \Delta x]^T \Sigma^{-1}_i [f_i(x_0) + J_i(x_0) \Delta x] \\ =\sum_i\frac{1}{2}[f_i(x_0)^T \Sigma^{-1}_i f_i(x_0) + 2\Delta x^T J_i(x_0)^T \Sigma^{-1}_i f_i(x_0) + \Delta x^T J_i(x_0)^T \Sigma^{-1}_i J(x_0)_i \Delta x] \tag {11}\] \[\frac{\partial F(x)}{\partial \Delta x} =\sum_i[ J_i(x_0)^T \Sigma^{-1}_i f_i(x_0) + J_i(x_0)^T \Sigma^{-1}_i J_i(x_0) \Delta x] = 0 \tag {12}\] \[\Delta x = \sum_i-[J_i(x_0)^T \Sigma^{-1}_i J_i(x_0)]^{-1}J_i(x_0)^T \Sigma^{-1}_i f_i(x_0) \tag{13}\]Final
The derivation process proves feasibility and provides insight into the specific mathematical transformation process, but in actual applications, more consideration should be given to
-
The performance of this method in solving large-scale problems,
-
How this method copes with local optimal situations and how convergent it is.
The former generally uses marginalization methods in SLAM due to sparse graphs; the latter requires deeper mathematical analysis and step size selection strategies. The following two aspects will be recorded separately.