SLAM-相机模型

针孔相机

VSLAM前端的核心目的是得到相机的位姿状态与环境信息，特征点法则是现有体系中VSLAM前端的主要方法之一，能够通过特征点在图像中位置的变化来得到位姿。其基本原理可以概述为，空间中一个固定的点在不同位置的相机中观测到的是不同的，那么我们可以根据其中的几何关系来推知不同位置的相机之间的位姿变换关系。（这句话本身并不严谨，但可以帮助理解，后文会有解释），为什么会不同？考虑以下单孔成像相机模型：

根据三角形相似原理，可轻易得出：

\[\left\{ \begin{matrix} x_i = f\frac{X_C}{Z_C} \\ y_i = f\frac{Y_C}{Z_C} \end{matrix} \right. \tag{1}\]

其中$x_i$、$y_i$为在单位图像坐标系下的投影。

但是因为$u$、$v$在呈现的图像上（Pixel Coordinate System），相较于单位图像坐标系（Image Coordinate System）是有缩放与位置的偏移，我们假设$x、y$轴上的缩放分别为$\alpha、\beta$,偏移分别为$c_x、c_y$,则：

\[\left\{ \begin{matrix} u=\alpha x_i+c_x \\ v=\beta y_i+c_y \end{matrix} \right.\tag{2}\]

那么很明显结合式（1）与（2）就可以得到图像上（Pixel Coordinate System）像素点与相机坐标系（Camera Coordinate System）下点的位置之间的关系：

\[\left\{ \begin{matrix} u=\alpha f \frac{X_C}{Z_C}+c_x \\ v=\beta f \frac{Y_c}{Z_C}+c_y \end{matrix} \right. \tag{3}\]

接下来，我们把$\alpha f、\beta f$ 分别设为$f_x、f_y$，并写成矩阵形式:

\[Z_C \begin{bmatrix}u\\v\\1\end{bmatrix} = \begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix} \begin{bmatrix}X_C\\Y_C\\Z_C\end{bmatrix} \tag{4}\]

但这时候，我们还要注意一点，

即：

\[P_{uv} = \frac{1}{Z_C}KP\]

此外，对于单目相机模型，我们默认$P_{uv}$已经经过畸变矫正（径向与切向）：

\[x'=x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2)\] \[y'=y(1+k_1r^2+k_2r^4+k_3r^6)+p_1(r^2+2y^2)xy+2p_2xy\]

径向的主要原因是透镜的安装，而切向畸变的主要原因是透镜与成像平面不完全平行。

双目相机

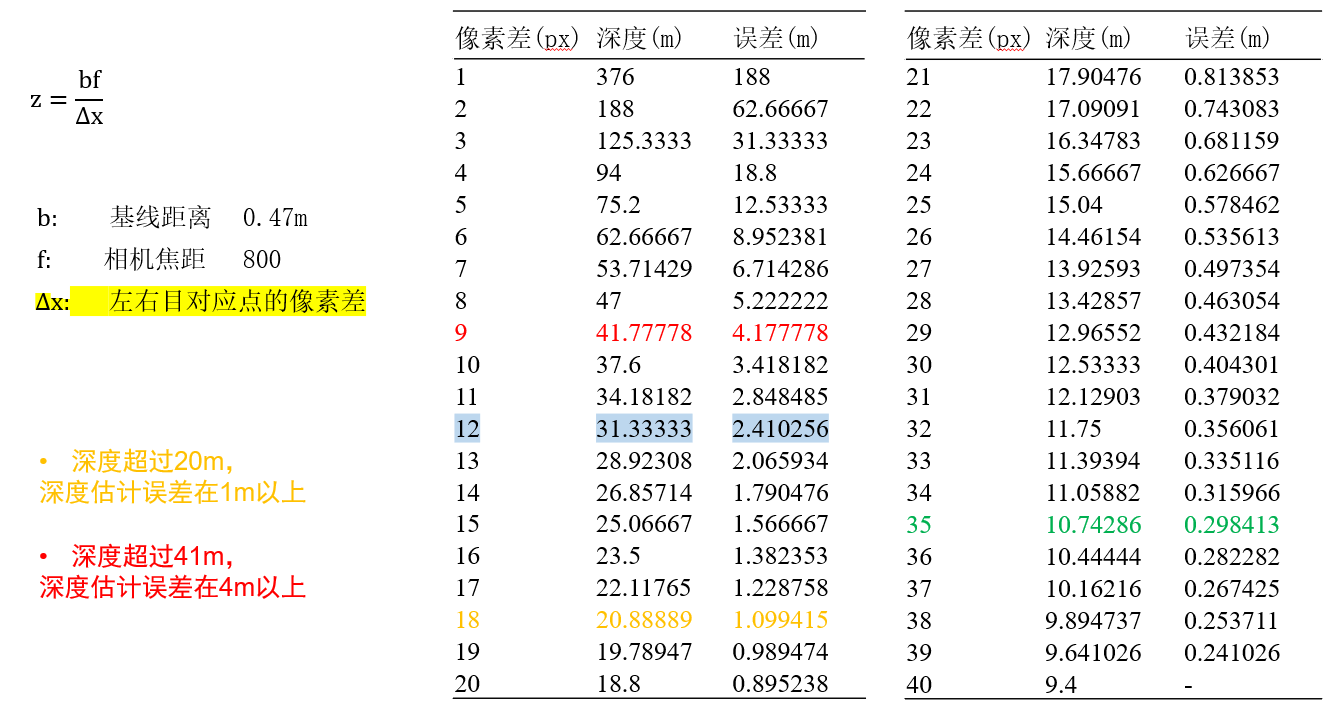
即两个相机的组合，可以通过测深度：

\[\frac{u_1-u_2}{b}=\frac{f}{z}\]

不过这部分的精度其实是有一定的问题（对于较远的目标1pix差可能差很多），同时base越大（即两个相机的平行距离），深度分辨率越强

​