dl-r-01线性多层与反向传播
在机器学习领域,仿射变换(带偏置的线性变换)是基础模型架构的核心,如 softmax 回归通过单一线性映射加激活函数实现分类。但线性假设存在显著局限:
- 单调性约束过强:例如收入与还款概率虽呈正相关,但非严格线性;体温与死亡率更呈现非线性的 “U 型” 关系,简单线性模型无法准确建模。
- 特征交互难以捕捉:图像分类场景中,单个像素的重要性依赖上下文(如相邻像素的组合),线性模型无法表征这种复杂关联,即便通过预处理也难以解决。
多层感知机结构
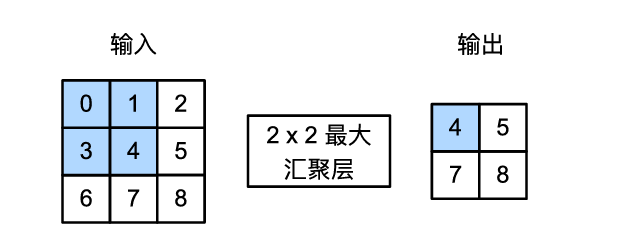
多层感知机就是指在输入层和输出层之间引入了一个或多个隐藏层,每个神经元与下一层的神经元全连接,通过激活函数引入非线性变换,从而具备了拟合复杂非线性函数的能力。
参考SoftMax的变化即增加了隐藏层:
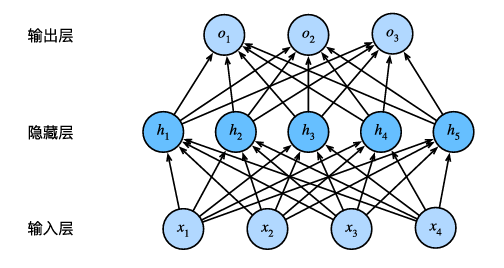
在神经网络中,隐藏层扮演着至关重要的角色。我的理解是通过非线性激活函数,将输入数据映射到更高维的特征空间,打破了线性模型的限制,每一层隐藏层去捕捉特征之间的复杂非线性交互,逐层提取越来越抽象的表达。一个不太恰当的例子去理解,在图像识别中,底层提取边缘,中层识别形状,高层理解物体语义。最终,经过多个隐藏层转换后,原始数据被“重塑”为一个可以被简单线性分类器区分的形式。

常见的几种激活函数有Sigmoid、tanh、ReLU,这里把函数及其导数形式都画了出来
/关于激活函数一般认为ReLU的优于另外两个,后续单开一个章节进行分析,事实上主要与其导数有关,工程上现在一般使用改进版本的ReLU/
训练手搓
那么使用pytorch构建多层感知机并识别fashion_mnist数据集:
import torch
from torch import nn
from torch.utils import data
import matplotlib.pyplot as plt
from d2l import torch as d2l
batch_size, lr, num_epochs = 256, 0.1, 50
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
net = nn.Sequential(nn.Flatten(),
nn.Linear(784,256),
nn.ReLU(),
nn.Linear(256,10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)
def accuracy(y_hat, y):
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis=1)
cmp = y_hat.type(y.dtype) == y
return float(cmp.type(y.dtype).sum())
net.train()
for epoch in range(num_epochs):
total_loss = 0.0
total_correct = 0
total_samples = 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y)
trainer.zero_grad()
l.mean().backward()
trainer.step()
total_loss += float(l.sum())
total_correct += accuracy(y_hat, y)
total_samples += y.numel()
train_loss = total_loss / total_samples
train_acc = total_correct / total_samples
print(f'Epoch {epoch+1}/{num_epochs}, '
f'Train Loss: {train_loss:.4f}, '
f'Train Acc: {train_acc:.4f}, ')
得到训练结果:
Epoch 1/50, Train Loss: 1.0378, Train Acc: 0.6438,
Epoch 2/50, Train Loss: 0.6003, Train Acc: 0.7877,
···
Epoch 48/50, Train Loss: 0.2389, Train Acc: 0.9144,
Epoch 49/50, Train Loss: 0.2359, Train Acc: 0.9170,
Epoch 50/50, Train Loss: 0.2356, Train Acc: 0.9151,
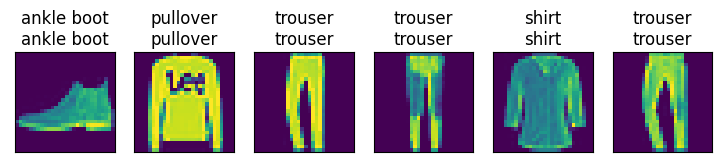
预测一下:
for X, y in test_iter:
break
trues = d2l.get_fashion_mnist_labels(y)
preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
d2l.show_images(X[0:6].reshape((6, 28, 28)), 1, 6, titles=titles[0:6])
在逐步接触到越来越深的模型训练的过程中,有下面几个问题需要讨论:
关于模型训练的泛化问题
这件事很值得考虑,因为我们训练一个模型是为了推理一种模式,而非通过训练调整参数得到训练数据的完美精度,这样才能做出有效的预测。这件事就类似于书中P140所述:
/假设一个大学生正在努力准备期末考试。一个勤奋的学生会努力做好练习,并利用往年的考试题目来测试自己的能力。尽管如此,在过去的考试题目上取得好成绩并不能保证他会在真正考试时发挥出色。例如,学生可能试图通过死记硬背考题的答案来做准备。他甚至可以完全记住过去考试的答案。另一名学生可能会通过试图理解给出某些答案的原因来做准备。在大多数情况下,后者会考得更好。/【好吧,本大学生有感觉被内涵到】
那么首先如何衡量模型训练的泛化程度?
我们通常将数据分为训练集与验证集,衡量训练loss与验证loss的大小,如果训练loss远小于验证loss则过拟合了
什么因素会导致模型泛化能力差?
-
可调整参数的数量。当可调整参数的数量(有时称为自由度)很大时,模型往往更容易过拟合。
-
参数采用的值。当权重的取值范围较大时,模型可能更容易过拟合。
-
训练样本的数量。即使模型很简单,也很容易过拟合只包含一两个样本的数据集。而过拟合一个有数百 万个样本的数据集则需要一个极其灵活的模型。【直接引用书中的部分了,简明扼要】
如何缓解过拟合问题
一个简单的做法即调整参数的数量,如对三个点拟合多项式调整多项式的阶数,但其实简单去限制丢弃特征很呆很不灵活,可以考虑两种技术
1、权重衰减(L_2正则化)
\[L(\mathbf{w},b)+\frac{\lambda}{2}\|\mathbf{w}\|^2 \tag{1}\]将原有的损失加上参数权重向量进行优化,可以防止权重过大缓解过拟合。
2、暂退法(Dropout)
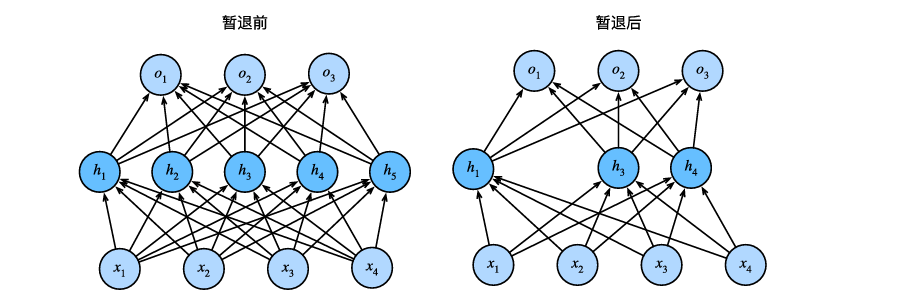
简而言之就是将某些单元的权重置为0。我的理解中这种方案考察的是一种鲁棒性
前向传播与反向传播
这里涉及到的内容是关于全连接的多层网络如何进行参数更新的,即训练过程梯度如何计算。
前向传播
第一步的前向传播即按照正向推理的方式得到最终的预测值,并利用预测值与构建的误差函数得到误差。
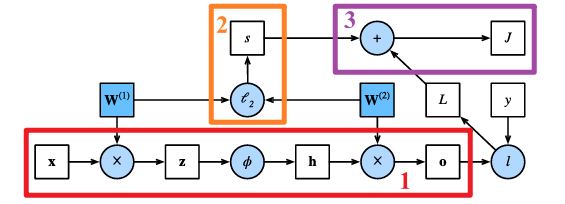
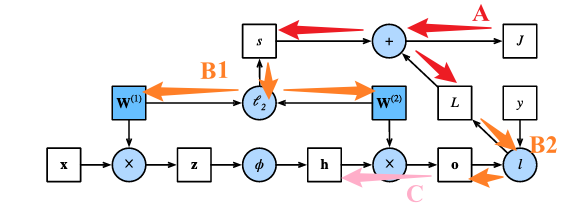
以上是一个二层网络的传播图,1部分包括:从输入样本$x$到第一层的中间变量$z$,经过激活函数$\phi$后得到第一层的输出$h$,最终得到第二层的输出$o$;2部分为正则化参数的正则化项计算;3部分得到最终的正则化损失$J$。这个$J$即为我们要优化的目标函数。
反向传播
反向传播即是计算神经网络参数梯度的方法,因为涉及到多层,所以直接对某一个参数进行求导显然工作量过大,但通过链式法则从输出层到输入层来遍历网络,中间存储所需要的偏导数。链式法则可以记为:
\[\frac{\partial \mathbf{Z}}{\partial \mathbf{X}} = \mathrm{prod} \left( \frac{\partial \mathbf{Z}}{\partial \mathbf{Y}}, \frac{\partial \mathbf{Y}}{\partial \mathbf{X}} \right)\]其中prod 是一个抽象符号,表示两个偏导之间的“乘法”,通常用于表示不同导数之间的组合,具体含义依赖于变量的结构维度。
以上述的计算图为例,我们要更新的网络参数为第一层参数$\mathbf{W}^{(1)}$与第二层参数$\mathbf{W}^{(2)}$,即计算$\frac{\partial{J}}{\partial{\mathbf{W}^{(1)}}}$与$\frac{\partial{J}}{\partial{\mathbf{W}^{(2)}}}$。
显然目标函数$J$与$s$和$L$都相关,故一步步向前传播:
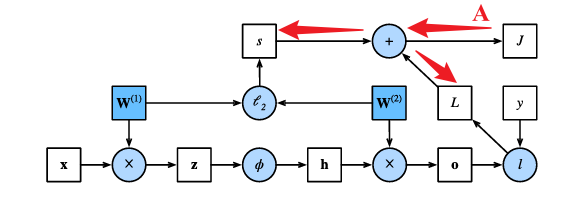
则计算正则化项相对于两个参数的梯度,以及计算目标函数关于输出层变量$o$的梯度:
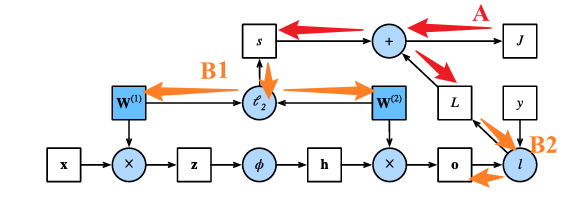
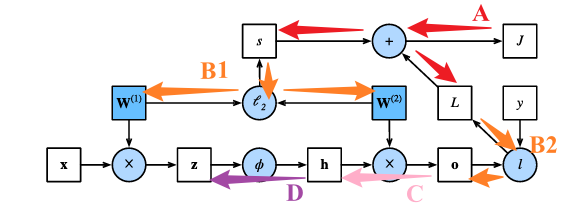
继续传播得到:
激活函数为按照元素计算的,所以这部分为按照元素的乘法运算符:
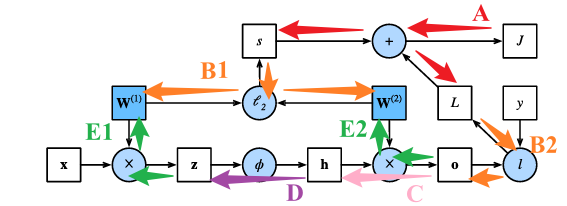
最终得到结果为B1与E的综合结果:
\[\frac{\partial J}{\partial \mathbf{W}^{(1)}} = \text{prod}\left(\frac{\partial J}{\partial \mathbf{z}}, \frac{\partial \mathbf{z}}{\partial \mathbf{W}^{(1)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(1)}}\right)=\frac{\partial J}{\partial \mathbf{z}}\mathbf{x}^\top+\lambda\mathbf{W}^{(1)}\] \[\frac{\partial J}{\partial \mathbf{W}^{(2)}} = \text{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{W}^{(2)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(2)}}\right)=\frac{\partial J}{\partial \mathbf{o}}\mathbf{h}^\top+\lambda\mathbf{W}^{(2)}\]