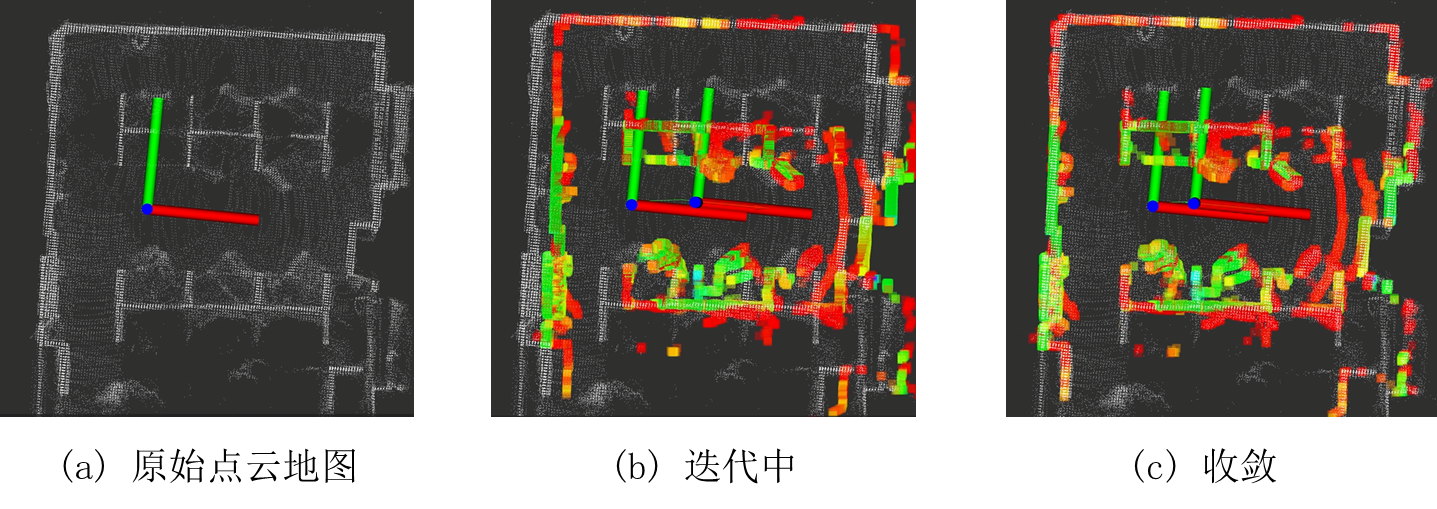
From high-dimensional Gaussian distribution to least squares

For high-dimensional Gaussian distribution $X\sim N(\mu,\Sigma)$,

\[f(X) = \frac{1}{\sqrt{(2\pi)^N\det(\Sigma)}}\exp [-\frac{1}{2}(X-\mu)^T\Sigma^{-1}(X-\mu)], \ X \in \mathbb{R}^{N} \tag 1\]

so,

\[P(X|Y_k) = N(\mu_k,\Sigma_k) \tag 2\]

Find the maximum likelihood estimate of the parameter $Y$ for observation $X$:

\[L(X_1,X_2,\cdots,X_n|Y_k) = \prod_if(X_i|Y) \tag 3\] \[\ln(L) = -\sum_i\ln\sqrt{(2\pi)^N\det(\Sigma_k)} -\frac{1}{2}\sum_i(X_i-\mu_k)^T\Sigma_k^{-1}(X_i-\mu_k) \tag{4}\]

Obviously, the first term is a constant term, and the second term affects the final result.

\[(Y_k)^*=\arg\max\ln(L) \\ =\arg\min (- \ln(L)) \\ =\arg\min\sum_i(X_i-\mu_k)^T\Sigma_k^{-1}(X_i-\mu_k) \tag 5\]

What does that look like? Least squares!