SLAM-惯性测量单元IMU的深入分析

IMU一般输出至少有六轴传感器信息，包括三轴的角速度（陀螺仪）以及三轴的线加速度（加速度计）。值得注意的是IMU的测量值依赖于惯性系，这个是由其测量模型决定的，同时IMU一般刚性安装在机器人（小车）上，且所以我们一般认为IMU输出的是机体坐标系下的惯性测量值。

测量模型

加速度计

首先对加速度计来进行分析；是如何测量得到加速度的呢？我们可以假设一个悬置的立方体，其上下左右链接了弹簧来支撑将其限制在固定位置(下左图)。当发生加速/减速运动时，由于惯性显然立方体会有一个运动趋势，此时弹簧被挤压受力(下右图)，此时假设我们能够准确测量出弹簧所受到压力，那么自然能够反推出立方体受到的力进而得到加速度。

值得注意的是，由于在地球上，一切物体受地球万有引力的影响，所以即使静止不动，弹簧也自然受到立方体的重力。如果刚体不是完全垂直于地平面（而非地面），那么这个重力也将不会垂直于Z轴（> 即我们说的IMU输出的是机体坐标系下的惯性测量值）。

以上就是加速度计的基本原理，当前由于微电子技术的发展，我们不使用这种立方体 + 弹簧的组合（你会注意到这个力的变化其实并不是一个冲激性的，因为弹簧会震荡），将其替换为另一种能够施加其上的固定电磁力。

那么显而易见的，我们可以得到如下的测量模型，来表示测量值与我们使用的加速度值之间的关系：

\[\widetilde{a}=R_W^B\left(a_{W}-g\right)+b_a+\eta_a\]

其中，$\widetilde{a}$为测量值；$a_{W}$为世界坐标系下的加速度（符合笛卡尔坐标系下运动）；$g = [0,0,-9.8067]^T$定义为重力加速度；$R_W^B$从世界坐标系旋转矢量到车体系的旋转矩阵，即车体位姿的转置（旋转矩阵正交）；$b_a$和$\eta_a$建模为IMU的测量噪声，分别表示高斯白噪声（高斯过程）与零偏（维纳过程）。

好吧，似乎并不显而易见~

我们从原理直接跳到结论确实是有几层跨度，那我们从头开始，首先我们不管噪声的影响，假设测量是完全准确的；同时从弹簧出发，利用牛顿第二定律：

\[F = am\]

将合力展开（这里定义的重力矢量与坐标轴反向）：

\[m\widetilde{a} + R_W^Bmg = a_Bm\]

进一步消去质量，并将重力右移：

\[\widetilde{a} = a_B - R_W^Bg\]

那么就只剩下噪声了，就是这样来的。当静止的时候你会发现，IMU的输出是正的，其实就是重力的影响。关于误差建模这部分我们后续再讨论，存在误差可以理解，但是误差为何建模成这样的方式值得讨论。

陀螺仪

陀螺仪我的感觉是很难描述，一个简单的理解就是我们幼年时代抽的那个陀螺，或者是飓风战魂？【是在胡言乱语】，我的理解是，一个高速运转的转子会永久的保持一个方向，三个环套在一起各自负责一个自由度，当外面的刚体转动的时候，这时候外面的轴也会跟着转动，我们测量转动轴的角度再除时间，就可以得到角速度了。

当然，同样的当下的MEMS（微机电系统）陀螺仪也不再使用这种巨大结构，转而感知转动时的科里奥利力（高中竞赛物理/大学物理复习一下？），无论如何，明确其感知到的角速度是机体系下的，明确这一点即可。

同样的，测量模型为:

\[{\widetilde{w}}_B=w_B+\ b_w+\eta_w\]

符号不再过多解释了。

误差分析

建模

所谓误差，即测量误差，我们不能保证测到的一定是准确的，甚至可以说人类本身所有的测量都是取一个近似值（开始哲学了），但是幸运的是，我们发明了从统计的角度去估计误差，即使存在各种假设和不确定性，但是通过引入统计量估计不确定性确实能使得我们更好的使用测量的数据。

这里定义了白噪声:

\[\eta\left(t\right)\sim N\left(0,\delta\left(dt\right)Cov\left(\eta\right)\right)\]

以及零偏（注意，这里是零偏的导数符合高斯过程，同时零偏本身的值一般不为0）：

\[\dot{b}\left(t\right)\sim N\left(0,\delta\left(dt\right)Cov\left(b\right)\right)\]

为什么这样建模？我的理解是我们将噪声的传播进行了假定处理，首先假设噪声服从高斯分布，并使用白噪声反应短时间内测量的不确定性的强度，使用零偏反应长时间中不确定性的随机变化趋势。怎么看出来的呢？

我们将上面的公式进行离散化，一般我们采集数据的过程是进行一段数据累计取平均，那么：

\[E(\eta^2) = E((\frac{1}{\Delta t} \int_{t_1}^{t_1+\Delta t} \eta\left(t\right)dt)^2)\]

将平方展开，并将E代入中心，对冲击函数求积分，最终得到：

\[E(\eta^2) = \frac{1}{\Delta t} Cov\left(\eta\right)\]

即离散形式：

\[\eta\left(k\right)\sim N\left(0,\frac{1}{\Delta t}Cov\left(\eta\right)\right)\]

对于零偏，一步一步去做最后得到：

\[b\left(k+1\right)\ -\ b(k)\sim N\left(0,\Delta t C o v\left(b\right)\right)\]

两者代表的不确定性已经很明显了。

标定

标定部分采用Allan方差，来分析得到零偏和白噪声，首先需要收集至少2h的IMU静置的数据（allan方差）。这部分涉及到一些信号分析的部分，确实不太擅长就不再从原理做分析了，我们只叙述allan方差的流程，并进行定性的分析。

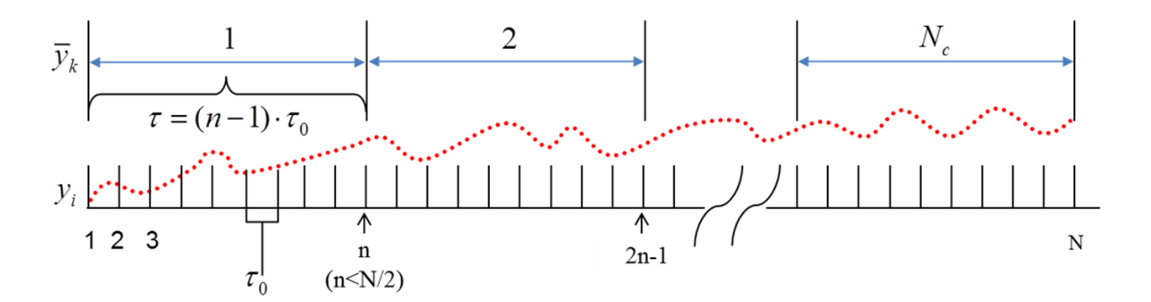
传统的求样本方差的方法可以反映误差序列的整体情况的指标，但无法细分出不同时间尺度上的误差波动情况。而allan方差通过分块处理 + 消除静态偏置的方法。我们要求不同时间尺度的误差分析，那么就将统计数据进行时间分块（块之间的时间尺度相同，但是做不同组实验的时候，时间尺度不同），收集到不同时间尺度对应的allan方差数据。具体公式为：

\[\sigma^2\left(\tau\right)=\frac{1}{2}E\left(\left({\bar{y}}_2-{\bar{y}}_1\right)^2\right)\]

${\bar{y}}_2$ 、${\bar{y}}_1$即相邻的时间块，最终取双对数，画图如下：

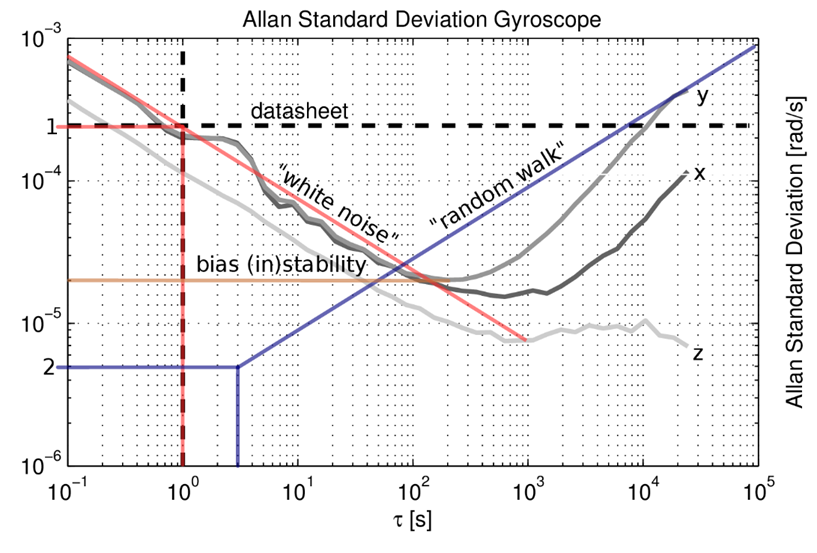
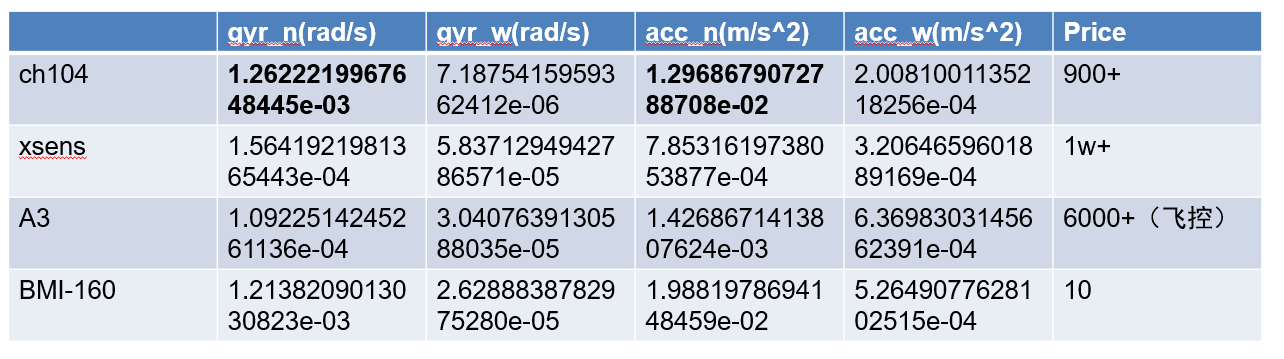
红色的线是标注的白噪声，呈斜率 - 1/2 的直线，蓝色的则是随机游走（零偏），呈斜率 + 1/2 的直线；注意这里的结果是离散时间的误差结果。通过${\bar{y}}_2-{\bar{y}}_1$消除静态偏置，当采样块时间短时，反应白噪声；$\bar{y}_2$的均值处理将白噪声变得很小。当采样块时间长时，反应零偏变化。以下是根据开源方法imu_utils测得的结果，可见一分价钱一分货：