SLAM-NDT

NDT算法的大名为Normal Distribution Transform，即正态分布变换，用于激光点云配准。算法的核心也正如其名，将目标点云按照体素（栅格）的方法划分，得到每个格子中点云的正态分布参数，再计算待配准点云在各个格子中的概率分布之和，这个值越大，那么配准结果越好。

下面简要复述一遍算法流程，再盘一盘各个流程中值得注意的点，以及提及我在实践算法中所遇到的问题。以后的经典算法Blog大致也将沿用这个流程~

算法流程

---

1） 构造目标点云的数据结构，按照设定分辨率分配到体素（栅格）中

2） 计算体素（栅格）中的点云高斯分布参数

3） 待配准点云完成配准

4） 构建无约束非线性优化，迭代求解

---

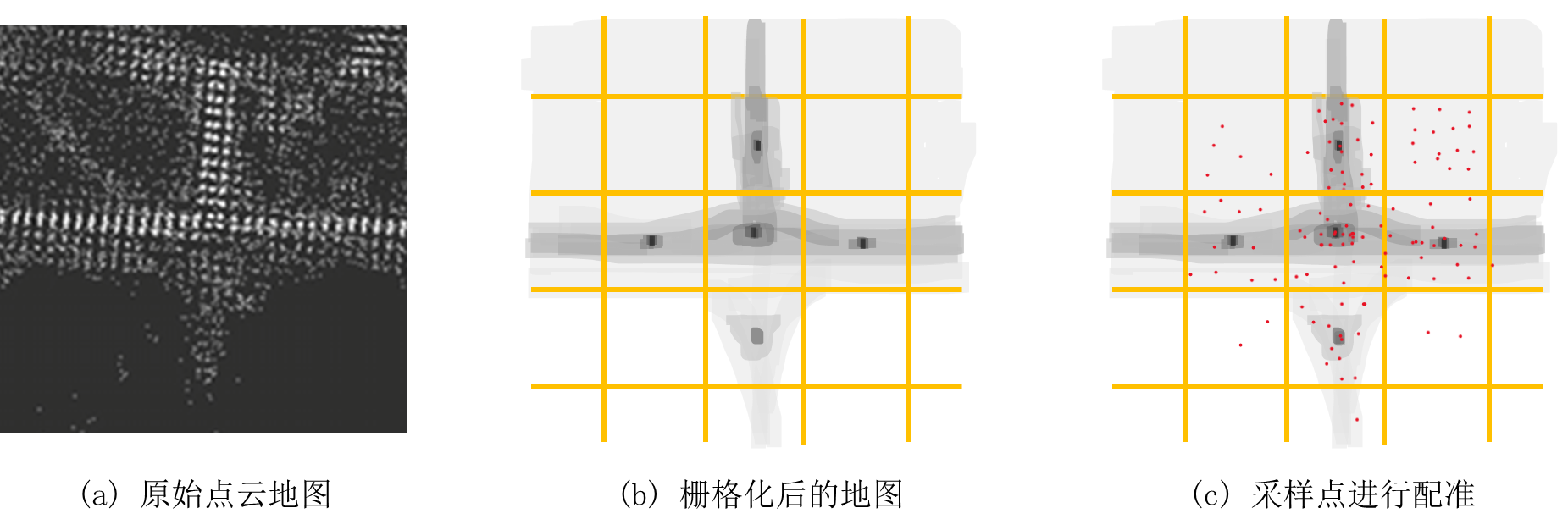
为了方便画图，用二维的栅格来表示，从原理上与体素是一致的，体素可以视为三维的栅格，即比栅格多了一个维度。图(b)中从白色到黑色表示点云概率分布越大，实际上存储我们只计算均值与协方差，这样可视化是为了更方便的理解。

数据结构的构建

这里选择的数据结构毋庸置疑了，算法流程都已经要使用到体素了，那么肯定是直接使用体素这种数据结构了，这里建议也自己参考高博的代码写一遍；在点云配准中数据结构的选择我认为是极为重要的，对于不同的场景实际上要选择不同的数据结构，增删查改的算法效率涉及到SLAM过程中最关注的实时性，尤其是在自动驾驶流形采用端到端的时代，SLAM的空间似乎越来越小了，其能拥有的资源是不是也越来越小了

关于设定分辨率这个部分我也想要多提一嘴，不一样的场景下分辨率大小的设定就不必再详细说了。在实际的工程项目中，未进行滤波前一个校园规模的点云地图就接近10GB，加载地图的过程中直接读取显然很不理想，除了切分再发布这种方案，如何更好的进行滤波也值得去考虑。

计算参数

在一个体素内我们认为其中的点云服从$N(\mu_k,\Sigma_k)$的高斯分布，其参数如此计算：

\[\mu_k = \frac{1}{N_k}\sum_i^{N_k}{p_i} \tag1\] \[\Sigma_k =\frac{1}{N_k-1}\sum_i^{N_k}(p_i - \mu_k)(p_i - \mu_k)^T \tag 2\]

这里是为了满足无偏性，是样本协方差，所以$N_k-1$！我看到一些推导没有减去那个1，大大地不对。

点云在哪个格子里

在体素的方法中，点云配准似乎很简单，计算落到哪个体素里就可以了。

优化问题构建与求解

显然从图(c)中很容易可以看出来，如果我们所有的待配准点云与结构中的越相似，那么说明我们的位姿表示的就越正确。具体到一个点就是距离哪个格子的均值越近那就越好，我们用协方差的逆作为信息矩阵加权也是常规操作了(分布的越散说明约不可靠，权越小)。对于在位姿$(R,t)$情况下，待配准点云中的第$j$个点$q_j$落在第$i$个体素中，参数为$\mu_j、\Sigma_j$，构造残差：

\[e_j = Rq_j + t-\mu_j \tag 3\]

则目标函数为：

\[(R,t)^* = \arg \min_{R,t} \sum_j{e_j^T\Sigma_j^{-1}e_j} \tag 4\]

如果我们选择使用高斯牛顿法求解，那么需要推得误差项关于状态变量的雅可比矩阵用于迭代，这里使用李代数右扰动求导：

\[\begin{aligned} \frac{\partial{e_j}}{\partial{R}} & =\lim_{\delta \phi \rightarrow 0} \frac{(R\exp(\delta \phi^\wedge)q_j + t-\mu_j) - (Rq_j + t-\mu_j) }{\delta \phi} \\ &=\lim_{\delta \phi \rightarrow 0} \frac{R(I + \delta \phi^\wedge)q_j - Rq_j}{\delta \phi} \\ &= \frac{-Rq_j^\wedge\delta \phi}{\delta \phi} \\ & = -Rq_j^\wedge \end{aligned} \tag 5\] \[\frac{\partial{e_j}}{\partial{t}} = I \tag 6\]

即：

\[J = \begin{bmatrix}-Rq_j & I\end{bmatrix}\]

那么接下来按照以下高斯牛顿的步长计算即可。

\[\Delta x = \sum_j-[J_j^T \Sigma^{-1}_j J_j]^{-1}J_j^T \Sigma^{-1}_j e_j \tag{13}\]

试验一下：

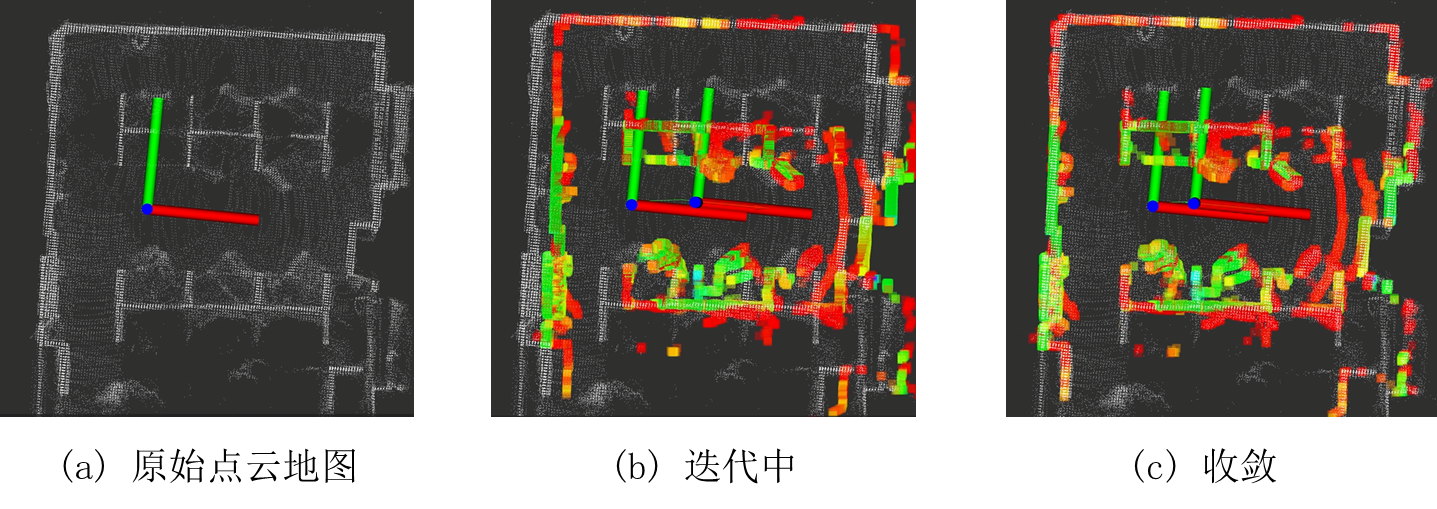
成功~