Relearn Linear Algebra: Vector Space

Regarding the concept of vector space, Wikipedia explains it as follows:

A vector space is a special set formed by a group of mathematical fields (such as real numbers or even functions) that can be scaled and added, with the unique characteristic that the resulting vectors after scaling and addition still belong to this set.

I find this perspective on understanding vector spaces quite fitting and decided to adopt it directly.

Vector Space and Subspace

Representation of Vector Space

Here, We will discuss vector spaces only in the context of real numbers, where vector spaces are represented as $\mathbb{R}^n$, with $n$ indicating the dimension of the vectors in the vector space. For ${v\in\mathbb{R}^1}$, $v$ can be any one-dimensional vector $\begin{bmatrix}x\end{bmatrix}$, for ${v\in\mathbb{R}^2}$, $v$ can be any two-dimensional vector $\begin{bmatrix}x \ y\end{bmatrix}^T$, and so forth. When we mention space, we can geometrically visualize $\mathbb{R}^1$ as a line, $\mathbb{R}^2$ as a plane, and $\mathbb{R}^3$ as the entirety of three-dimensional space, While we cannot imagine higher dimensions, we can remember that the vectors belonging to a vector space, after scaling and addition, still belong to this set.

Subspace

The concept of subspace is significant within vector spaces. Simply put, a subspace is also a vector space that depends on another vector space. When we mention “sub,” it implies that a set of vectors is contained within its dependent vector space $S$ and meets the conditions required to form a vector space. Thus, it can be termed a *subspace of vector space $S$.

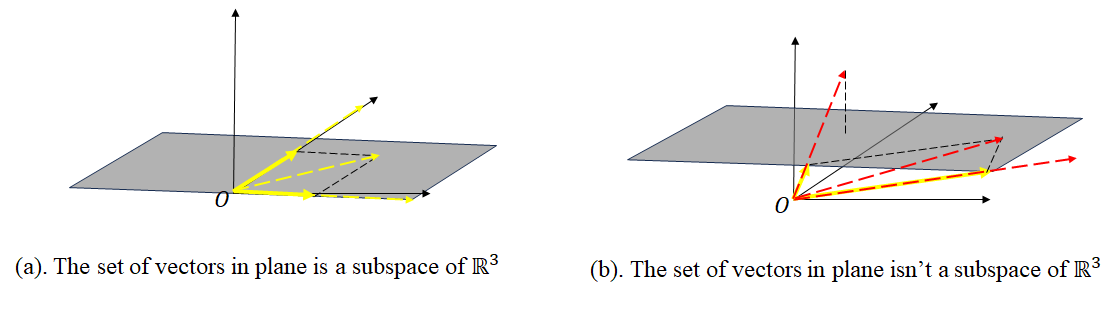
In the two scenarios below, according to the above rules, it is clear that (a) is a subspace of $\mathbb{R}^3$, while (b) is not.

Column Space and Null Space

For an $m×n$ real matrix $A$, its column space is the subspace of $\mathbb{R}^m$ generated by all the column vectors of the matrix $A$, denoted as $C(A)$.

The null space of an $m×n$ real matrix $B$ is the set of all solutions $v$ to the equation $Bv=0$, denoted as $\mathrm{Null}(B) $.